
Fundamentos de Biomecánica – Parte 3.
Raúl
Amil
3.1.
Partícula
Para simplificar
el análisis del movimiento vamos a considerar un cuerpo muy pequeño denominado
partícula, la cual es un punto, es
decir que no tiene tamaño, aunque si masa.
3.2.
Movimiento
El
movimiento es el cambio de posición de un cuerpo en el espacio. Si no tenemos
en cuenta las causas que lo producen, la ciencia que se encarga de su análisis
es la Cinemática, también llamada “geometría del movimiento”.
Al
movimiento general se lo puede clasificar según la trayectoria de las partículas
del cuerpo sujeto a análisis. Por lo tanto, según este criterio, podemos
dividir al movimiento general en traslación
y rotación (Figura 1).
 |
|||||
 |
|||||
 |
|||||
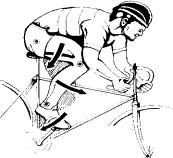
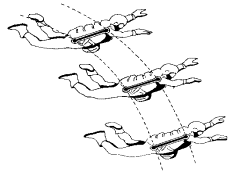
Figura 1: Movimiento
general
Movimiento de rotación
Movimiento de traslación
(de “The Biomechanics of Sports Techniques”, de Hay)
Veremos luego que también se puede clasificar al movimiento en función de la
velocidad, de lo que resultan el movimiento de velocidad
uniforme y el de velocidad variable.
Este último a su vez, puede dividirse en acelerado, desacelerado (ambos
uniformes o variables), y combinaciones de los dos.
3.3.
Movimiento de traslación
Se dice que el
movimiento de un cuerpo es de traslación,
si cada una de sus partículas experimenta el mismo desplazamiento que las demás
en un intervalo de tiempo dado.
El movimiento de traslación puede ser rectilíneo
o curvilíneo.
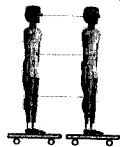 |
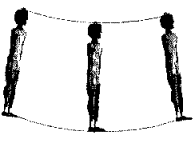 |
Figura 2: Movimiento rectilíneo
Movimiento curvilíneo
(de
“Biomecánica Deportiva”, de Gutiérrez Dávila)
3.4.
Desplazamiento
Analicemos el
movimiento de un corredor (Figura 3), y simplifiquemos el análisis al estudio
del desplazamiento de una determinada partícula de su cuerpo a la que
llamaremos CG (más adelante veremos
que se trata de su centro de gravedad).
Consideremos la posición de la partícula CG
definida por el vector de posición r1
en el instante t1. Un cierto tiempo después, o sea en el instante t2,
la posición de la partícula puede ser definida por el vector de posición r2.
El vector que define el desplazamiento de CG
se denomina vector de desplazamiento Dr, y se lo
calcula:
Dr = r2 - r1
 |
Figura
3 (de “Biomecánica Deportiva”, de Gutiérrez Dávila)
Dada la
característica vectorial del desplazamiento, este puede ser expresado:
r=
ix + jy
3.5.
Velocidad
La velocidad
de una partícula es la rapidez con la
que cambia de posición al transcurrir el tiempo.
3.5.1.
Velocidad media
Consideremos
nuevamente al corredor de la Figura 3. Según la definición anterior de
velocidad, podemos decir que la velocidad
media de CG puede calcularse como
el cociente del cambio de posición o desplazamiento Dr y el
intervalo de tiempo transcurrido (Dt = t2 – t1).
v
= Dr/Dt
La cantidad v es un vector, ya
que se obtiene dividiendo un vector por un escalar, y su dirección y sentido es
el de Dr. En
Biomecánica la unidad utilizada para la velocidad es metros por segundo (m/s).
Nótese
que para definir v, no nos
interesó si la trayectoria de CG
ocurrió en línea recta o curva, sino que analizamos las posiciones inicial y
final de dicha partícula. Es por esta razón que a v se la llama velocidad
media.
3.5.2.
Velocidad instantánea
Supongamos
que la partícula CG del corredor de
la Figura 4 se está moviendo de tal manera que su velocidad media medida en un gran número de intervalos no resulta
constante, por lo tanto se puede decir que CG
se mueve con velocidad variable. A la
velocidad de CG en un instante
cualquiera se la denomina velocidad
instantánea, y se la define según la ecuación (ver nota 1, párrafo
1.6.2):
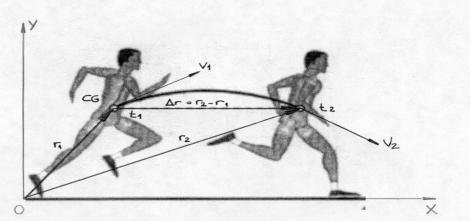 |
Figura 4 ((de “Biomecánica Deportiva”, de Gutiérrez Dávila)
v
= Lim Dr
/ Dt
= dr/dt
Dt ![]() 0
0
Dada la característica vectorial de la velocidad, esta puede ser expresada:
v=
ivx + jvy
v = dr/dt, Þ
v = idx/dt + jdy/dt
En el siguiente gráfico podremos ver las diferentes posibilidades de comportamiento de la velocidad en función del tiempo.
 |
3.6.
Aceleración
Cuando
la velocidad de una partícula cambia, ya sea en magnitud, en dirección, o en
ambas, se dice que dicha partícula posee aceleración. Por lo tanto podemos
definir a aceleración de una partícula
a la rapidez con que cambia su velocidad en función del tiempo.
3.6.1.
Aceleración media
Analizemos
nuevamente a la partícula CG del
corredor de la figura 4. Su velocidad instantánea en el instante t1
es v1 . En el instante
posterior t2 estará moviéndose con una velocidad instantánea v2.
La aceleración media de CG,
se la define como el cambio de velocidad (Dv
= v2 - v1)
en el intervalo de tiempo (Dt = t2 – t1 ), por lo tanto:
a
= Dv/Dt
La
cantidad a es un vector ya que
se obtiene dividiendo un vector por un escalar, y su dirección y sentido es el
de
Dv. La
unidad utilizada para la aceleración es metros por segundo al cuadrado (m/s2).
3.6.2.
Aceleración instantánea
Si la
partícula CG se está moviendo de
tal manera que su aceleración media, medida en intervalos de tiempo diferentes
no es constante, entonces decimos que CG
se mueve con aceleración variable.
Análogamente,
a la velocidad, podemos definir a la aceleración en un instante determinado
como aceleración instantánea,
definida por la expresión:
a
= Lim Dv
/ Dt
= dv/dt
![]() 0
0
Dada la
característica vectorial de la aceleración, esta puede ser expresada:
a=
iax + jay
a = dv/dt, Þ
a = idvx/dt
+ jdvy/dt = id2x/dt2
+ jd2y/dt2
En el
siguiente gráfico podremos ver las diferentes posibilidades de comportamiento
de la aceleración en función del tiempo.
|
|
(de
“Biomecánica Deportiva”, de Gutiérrez Dávila)
3.7.
Relación entre variables cinemáticas cuando la aceleración es constante
En los
casos en que la aceleración de los cuerpos sujetos a análisis la aceleración
se mantenga constante, como es el caso de los implementos del atletismo luego
del saque final, o el cuerpo de los saltadores luego de efectuar su batida, es
útil conocer las ecuaciones que relacionan la velocidad y la posición.
Por
ejemplo de la fórmula de aceleración tenemos que: a=
Dv / Dt
= (vf –vi)
/ (tf – ti)
Considerando
ti = 0, para el comienzo del movimiento y despejando tenemos que:
vf
= vi + at (1)
v
= Dr/Dt
= (rf –ri)
/ (tf – ti) = rf/tf = r/t
Despejando obtenemos: r = v.t
Por otra
parte v = (vf
+ vi)/2
Þ
r = 1/2(vf
+ vi)t
Reemplazando
la ecuación (1) en la de r tenemos
que:
v2f
= v2i + 2a.r (3)
Las
ecuaciones (1), (2), y (3), nos permiten un detallado análisis del movimiento
cuando la aceleración permanece constante, y también se aplican en los casos
de tiro vertical y caída libre de objetos, con el reemplazo de a
por g, que es la llamada aceleración gravitatoria y tiene un valor
absolutode 9.81 m/s2.
3.8.
Movimiento de los proyectiles
En
varias disciplinas deportivas es común arrojar o impactar elementos, los cuales
una vez en el aire, (despreciando la resistencia del mismo y otras fuerzas
externas), desarrollan un movimiento bidimensional de aceleración constante g
dirigida hacia abajo (no hay componente horizontal de la aceleración).
Dadas
estas características, el movimiento de cualquier proyectil, como un disco, una
pelota de fútbol, o el cuerpo de un saltador luego de efectuar su batida, puede
describirse utilizando las ecuaciones (1), (2), y (3), del parágrafo anterior.
Supongamos
el lanzamiento de la bala (Figura 5), considerada como una partícula, que es
arrojada con una velocidad v0,
un ángulo q0,
y que alcanza una distancia R:
|
|
Figura
5 (de Física I, de Resnick y Halliday)
Las
componentes de v según los ejes X e Y son:
vx0 = v0.cosq0 vy0 = v0.senq0
Como no
hay componente horizontal de la aceleración, la velocidad horizontal permanecerá
constante hasta el momento del impacto contra el suelo (esto explica porque la
bala comienza a rodar una vez que cae). Su expresión según la ecuación (1)
será:
vx
= v0.cosq0
La
distancia R que alcanzará se puede deducir de la (2):
r =
vi.t + ½ at2
Reemplazando:
R
= v0.cosq0.T
El
tiempo de vuelo será la suma del tiempo que tarda el proyectil en subir más el
que tarda en bajar, entonces:
T
= tsubir + tbajar = 2t
De la
(1):
vf
= vi + at
Como vf
= 0, y a = -g, reemplazando:
0
= v0.senq0
– g.t Þ
t= v0.senq0/g
Por lo
tanto:
T
= 2 v0.senq0/g
Reemplazando:
R
= (v20.2cosq0.
senq0)/g
Dado que
2cosq0.
senq0
= sen2q0,
sustituyendo en la anterior:
R
= (v20.sen2q0)/g
De esta ecuación se puede deducir que la distancia alcanzada por un
proyectil será mucho más sensible a las variaciones de velocidad de salida que
a las del ángulo de disparo, así como también que el ángulo de salida que
maximiza el valor de R es 45º (sen 90º = 1).
En el caso de que quisiésemos calcular la altura máxima que podría
alcanzar el punto CG de un saltador de altura (Figura 6), podemos utilizar la
ecuación (2):
r =
vi.t + ½ at2
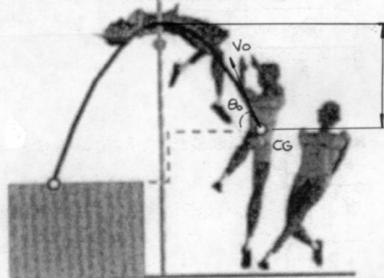 |
Figura
6 (de “Biomecánica Deportiva”, de Gutiérrez Dávila)
Donde: r
=H;
t = tsubir = v0.senq0/g;
vi = v0.senq0;
a = -g
Por lo
tanto:
H = (v02.sen2q0)/g
– ½(v02.sen2q0)/g
H
= (v02.sen2q0)/2g
3.9.
Movimiento de rotación
Un
cuerpo describe un movimiento de rotación
pura si todas sus partículas se
mueven en círculos, y los centros de esos círculos se encuentran en una línea
recta denominada eje de rotación.
No es
usual que en la actividad deportiva se presente el movimiento en forma de rotación
pura, sino que como habíamos mencionado en el parágrafo 3.2., al movimiento
general se lo podía descomponer en rotación y traslación. Un ejemplo de ello
es el movimiento que posee el Disco luego del saque final.
Las
variables utilizadas para describir el movimiento de rotación son semejantes a
las del movimiento de traslación, por lo cual tenemos desplazamiento angular, velocidad angular media, velocidad angular
instantánea, aceleración angular media, y aceleración angular instantánea.
3.10.
Desplazamiento angular
La
posición angular de una partícula elemental P girando alrededor de un eje de
rotación fijo, se define por el ángulo q,
el cual se mide en radianes (rad).
Arbitrariamente se considera positivo cuando se lo mide en sentido antihorario.
Supongamos
que la posición de la partícula elemental P en el instante t1 sea q1
(Figura 7). Luego de un tiempo, en el instante t2, la nueva posición
de P está definida por q2.
El desplazamiento angular de P será:
Dq
= q2
- q1
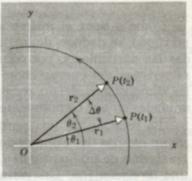
3.11.
Velocidad angular media
El
intervalo de tiempo que la partícula P utilizó para pasar de la posición q1
a la q2,
es Dt
= t2 - t1. Se define como velocidad angular media al
cociente entre el desplazamiento angular y el intervalo de tiempo empleado para
dicho desplazamiento.
w
= Dq
/ Dt
La
unidad empleada en Biomecánica es rad/seg.
3.12.
Velocidad angular instantánea
La velocidad
angular instantánea w
se define como el límite del cociente entre el desplazamiento angular y el
intervalo de tiempo cuando este tiende a cero.
w
= Lim Dq /
Dt
= dq/dt
Dt ![]() 0
0
3.13
Aceleración angular media
Si la velocidad angular de P no es constante, entonces la partícula
tiene aceleración angular. Si en el instante t1 la velocidad angular
instantánea de P es w1,
y en el instante t2 es w2,
se define como aceleración angular media al cociente:
a
= (w2
- w1)/(t2
- t1) = Dw
/ Dt
La unidad utilizada en Biomecánica es rad / seg2.
3.14.
Aceleración angular instantánea
La aceleración
angular instantánea es el límite de la variación de velocidad cuando el
intervalo Dt
tiende a cero.
a
= Lim Dw /
Dt
= dw/dt
Dt ![]() 0
0
3.15.
Relación entre variables cinemáticas cuando la aceleración angular es
constante
Procediendo
análogamente al parágrafo 3.7., podemos obtener las siguientes relaciones
equivalentes a las ecuaciones (1), (2), y (3):
wf
= wi
+ at
(4)
q = wi.t
+ ½ at2
(5)
w2f
= w2i
+ 2a.q
(6)
3.16.
Las cantidades rotacionales como vectores
En los
parágrafos 3.4., 3.5., 3.6., habíamos mencionado respectivamente que el
desplazamiento, la velocidad, y la aceleración lineal, eran cantidades
vectoriales. Dado que hasta el momento hemos considerado que la rotación se
producía alrededor de un eje fijo, por lo cual hemos podido considerar a q,
w,
y a
como escalares.
Se puede
demostrar que los desplazamientos
angulares finitos no son vectores pues no cumplen la conmutividad de la suma
(q1
+ q2)
¹
(q2
+ q1).
Por otra
parte, si los desplazamientos angulares se hacen muy pequeños, comienza a
cumplirse la ley de conmutabilidad de la suma, por lo tanto los desplazamientos
angulares infinitesimales son vectores.
De lo
anterior podemos deducir que si la velocidad angular instantánea es un cociente
entre un vector y un escalar, entonces dicha magnitud es un vector. Aplicando la
regla de la mano derecha, podemos obtener el sentido de w (Figura
8).
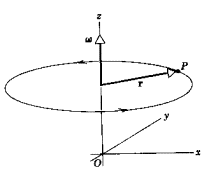
Figura
8 (de Física I, de Resnick y Halliday)
Análogamente
podemos decir que la aceleración angular instantánea también es una cantidad
vectorial.
3.17.
Relación entre los movimientos de rotación y traslación
Se
pueden demostrar las siguientes relaciones para una partícula P que gira con
una velocidad angular w,
alrededor de un eje fijo con un radio de giro r y una aceleración angular a:
Entre la
longitud de arco s y su posición angular q
(Figura 9):
s
= q.r
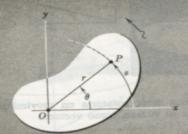 |
Figura
9 (de Física I, de Resnick y Halliday)
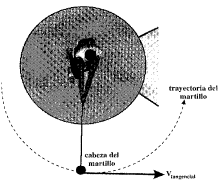
Entre la velocidad tangencial v y la angular w
(Figura 10):
v
= w.r
(escalar) ó v = w
x r (vectorial)
 |
3.17.1.
Aceleración tangencial y aceleración radial
La existencia del movimiento circular es posible gracias a dos fuerzas,
una tangencial y otra radial o centrípeta, que generan sus respectivas
aceleraciones at (tangencial), y ar
(radial) respectivamente (Figura 11). La suma vectorial de ambas es la aceleración
total a.
a = at
+ ar
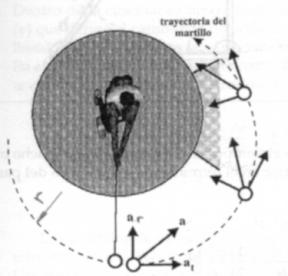 |
Figura
11 (de “Biomecánica Deportiva”, de Gutiérrez Dávila)
Asimismo se pueden demostrar las siguientes relaciones:
Entre la aceleración tangencial at y la angular a:
at
= a.r
ó at = a x r
(vectorial)
Entre la aceleración radial ar y las velocidades w
y v:
ar
= v2/r = w2.r
(escalar) ó ar = w x v
(vectorial)
Bibliografía utilizada:
RESNICK,
R., HALLIDAY, D. Física I. Cecsa,
1978
GUTIERREZ
DAVILA, M. Biomecánica Deportiva. Editorial
Síntesis, 1998
RASCH,
P. Kinesiología y Anatomía Aplicada. El
Ateneo, 1991
HAY,
J.G. The Biomechanics of Sports Techniques. Prentice-Hall,
1993
Ing. Raúl
J. Amil
rauljamil@hotmail.com