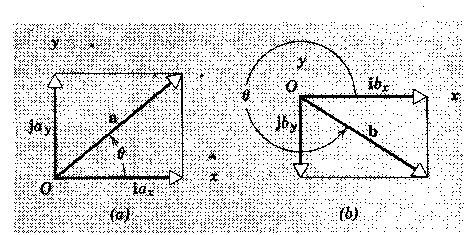
Figura 1: Representaciones gráficas de vectores y sus componentes rectangulares (de "Física I" de Halliday y Resnick)
Fundamentos de Biomecánica - Parte 2.
Ing. Raúl J. Amil
2.1. Magnitudes escalares y vectoriales.
|
|
|
Figura 1: Representaciones gráficas de vectores y sus componentes rectangulares (de "Física I" de Halliday y Resnick) |
Para
el caso de la Figura 1 a), las componentes rectangulares del vector a
resultan ser ax y ay, las cuales podemos determinar por
las expresiones:
ax
= a.cosq
ay = a.senq
Siendo q
el ángulo que forma el vector a con el sentido positivo
del eje de abscisas (x), medido en sentido contrario a las agujas del reloj.
Asimismo aplicando el Teorema de
Pitágoras y trigonometría respectivamente, podemos hallar el módulo del
vector a, y el ángulo q
a2
= ax2 + ay2
tgq
= ay/ax
En los sistemas de coordenadas rectangulares se suelen utilizar los símbolos i,
j, y k
para definir los vectores unitarios en las direcciones positivas de los ejes x, y, y z
respectivamente, por lo que los vectores a
y b de la Fig 1 también se pueden expresar:
a=
iax + jay
b = ibx + jby
2.2.
Álgebra vectorial
2.2.1.
Suma de vectores: Métodos geométrico y analítico
 .
.
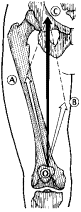
La suma de vectores por el método geométrico o del
paralelogramo requiere la representación a escala de los vectores sumando, y
consiste en trazar paralelas a los respectivos vectores, hasta lograr su
intersección. El vector resultante es la diagonal del paralelogramo
obtenido.(Figura 2).
Figura 2: Composición de fuerzas por el método del paralelogramo. El vector A representa la porción lateral del cuádriceps, mientras que el B representa la porción medial. (de "Kinesiología y Anatomía Aplicada", de Rasch).
Cuando sumamos más de dos vectores, es más práctico utilizar el denominado polígono de fuerzas, el cual se obtiene uniendo el extremo de un vector con el origen del siguiente. El vector resultante tiene su origen coincidente con el del primero, y su extremo con el del último (Figura 3).
|
|
|
Figura 3: Fuerzas interactuantes durante el desplazamiento de un nadador. (de "Biomecánica Deportiva", de Gutierrez Dávila) |
La suma de vectores por el método analítico consiste en
la suma algebraica de sus componentes rectangulares. Por ejemplo si el vector c es la resultante de la suma de los vectores a+b, entonces:
cx
= ax+bx
cy = ay+by
c2 = cx2 + cy2
tgq
= cy/cx
c
= i(ax+bx) + j(ay+by) = icx + jcy
La suma de vectores cumple las propiedades asociativa y
conmutativa, por lo tanto:
a+b = b+a
(asociativa)
d+(e+f) = (d+e) + f (conmutativa)
Por otra parte, la resta de vectores, por ejemplo a-b,
se realiza sumándole a a el opuesto
de b:
a-b = a+ (-b)
2.2.2.
Multiplicación de un vector por un escalar
El
producto de un cierto escalar k, y de
un vector a se escribe ka
y se define como un nuevo vector cuya magnitud es k veces mayor que la
magnitud de a.
2.2.3.
Producto escalar
Sean a
y b dos vectores cualquiera que forman un cierto ángulo q.
Se define como producto escalar de ambos, al producto de sus módulos por el
coseno del ángulo que forman.
a . b
= a.b.cosq
El
resultado del producto escalar de vectores es un escalar que puede ser positivo,
negativo o nulo (si
q
= 90º).
Asimismo
se puede demostrar que: a . b = axbx
+ ayby
Por
lo cual si conocemos las componentes rectangulares que definen dos vectores en
el espacio, y combinando las expresiones anteriores podemos conocer el ángulo
que ellos forman (Figura 6).
cosq
= (axbx + ayby)/a.b
Esta propiedad es muy utilizada en Biomecánica Deportiva para definir el desplazamiento angular en las técnicas cinematográficas, o bien para el cálculo del trabajo mecánico, el cual como veremos más adelante, es resultante del producto escalar de los vectores fuerza y desplazamiento.
|
Figura 4: Ejemplo de determinación del ángulo formado por los segmentos brazo y antebrazo conociendo los vectores que definen la posición de ambos.
|
|
El
producto escalar también goza de la propiedad conmutativa:
a
. b
= b . a
2.2.4. Producto vectorial.
c = a x b = a.b.senq
La dirección de c es perpendicular al plano formado por a y b. Para definir el sentido de c empleamos la "regla de la mano derecha", que dice que si se coloca la mano derecha de tal manera que los dedos cerrados sigan la rotación de a hacia b, el pulgar extendido apunta hacia en el sentido de c (Figura 5b). También podemos decir que el sentido de c es el de un tornillo de rosca derecha cuando se lo hace girar de a hacia b (Figura 5a). El producto vectorial es nulo cuando el ángulo q es 0º (vectores paralelos)
|
|
|
Figuras 5a, y 5b: Dirección y sentido del vector c (de Física I de Halliday y Resnick) |
De la definición de producto vectorial se puede también llegar a la expresión:
c = a x b = (iax + jay + kaz) x (ibx + jby + kbz)
c = a x b = i(aybz – azby) + j(azbx – axbz) + k(axby – aybx)
Lo cual se puede escribir en forma compacta como un determinante

El producto vectorial no
goza de la propiedad conmutativa por lo que: a x b = -b x a
Bibliografía utilizada
:MERIAM, J. Dinámica. Editorial Reverté, 1984
GUTIERREZ DAVILA, M. Biomecánica Deportiva. Editorial Síntesis, 1998
RASCH, P. Kinesiología y Anatomía Aplicada. El Ateneo, 1991